Wenn die Schülerinnen und Schüler Ideen zu schmückenden Belägen aus dem Morgenland entwicklen sollen, wird es schnell beliebig, weil ihnen die mathematische Strenge des Orients fehlt.  Hier können die Parkettierungen von Roger Penrose weiterhelfen. Mit nur zwei Grundbausteinen, die Penrose auf der Basis des “Goldenen Schnitts” aus einem Fünfeck entwickelt hat, lassen sich unendliche Ornamente erzeugen.

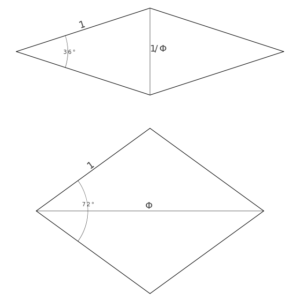
Es gibt mehrere verschiedene Sätze von Penrose-Kacheln; wir haben einen Satz gewählt, der sich besonders gut aus Fliesen schneiden lässt. Er besteht aus zwei Rauten, die gleiche Seitenlängen, aber unterschiedliche Eckwinkel haben:

• die erste Kachel, die dünne Raute, hat Eckwinkel von 36° und 144°,
• die zweite Kachel, die dicke Raute, hat Eckwinkel von 72° und 108°

Alle Winkel sind also Vielfache von 36°. Beide Kacheln stehen in Verbindung zum goldenen Schnitt Φ, bei der

• dicken Raute hat die lange Diagonale die Länge: Φ = 1/2 * (1+√5)
• die Länge der kurzen Diagonale der dünnen Raute ist  1/Φ.

Das Flächenverhältnis der beiden Rauten ist ebenfalls Φ, ebenso das Anzahlverhältnis der bei der Parkettierung insgesamt verwendeten Kacheln.

Drachen und Rauten:

Mit den Rauten haben die Schüler und Schülerinnen dann ihre “orientalischen” Mosaike gestaltet.

Im Bildungszentrum Butzweilerhof haben die angehenden Fliesenleger ihre Entwürfe umgesetzt. Unter der fachkundigen Aufsicht von Herrn Welter mussten sich die Schüler in Geduld und Präzision üben. Schließlich waren viele Rauten mit dem Glasschneider herzustellen und Ungenauigkeiten wurden beim Zusammenfügen direkt bestraft. Die Ergebnisse können sich aber sehen lassen.